Now that we know the basics of directed acyclic graphs, we’re going to move to a more specialized data structure, one that is wholly derivable from a DAG.

A topological ordering of a directed graph G = (V, E) is a linear ordering such that for every directed edge u -> v in E, u precedes v (in the linear ordering).

Example: Getting Dressed

For those of you who need an algorithm to figure out how to put your clothes on in the morning, you’re saved! Let’s define the task dependency graph for getting dressed. An edge x -> y in this graph means “you must put on x before y“, i.e. socks -> shoes is an edge, because you must put on your socks before your shoes.

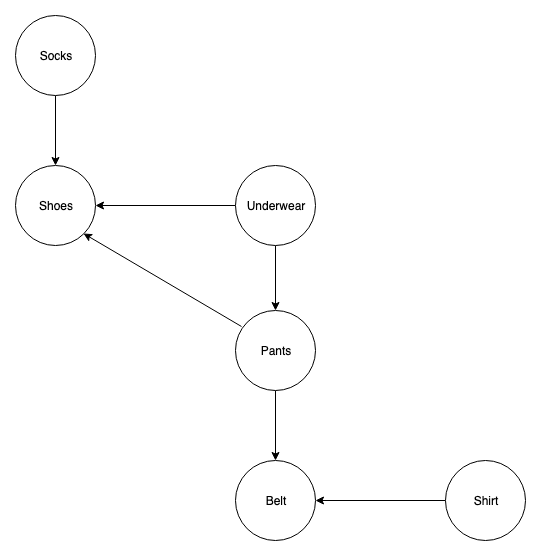
Without going into the details of how the topological sorting algorithm works (algorithm here), let’s run it on the graph.

We’ll use the tsort command, which has this implemented already implemented on most Unix based platforms. (As you can see below, we just provide space-separated tuples representing all edges in the graph).

tsort <<EOF
underwear shoes
socks shoes
underwear pants
pants belt
shirt belt
EOF

# output - a valid way to get dressed
shirt
socks
underwear
pants
shoes
belt

Note that topological orderings are not guaranteed to be unique. (You could put your shirt or socks on first, right? It doesn’t matter).

Also notice that the notion of a cycle in this graph makes no sense. (e.g. “You must put on your socks before your shoes, and your shoes before your underwear, and your underwear before your socks.” Good luck with that one).