Consistent Hashing
While reading a few days ago, I came across an interesting problem.
In load balancing, we want to evenly distribute the traffic to a number of servers. Cool, use a hash function, like mod (e.g. 8 % 3 = 5).
But here’s the catch — when we add a new server to the bunch, we don’t want to re-index existing traffic. In other words, the only traffic we want to re-distribute is the traffic that will be directed at the new server.
A mod function does absolutely terrible here; it’s guaranteed to be inconsistent (it would shift the result for every input). Now we’re in the world of consistent hashing.
Intuition
Say you have 4 servers. We’re going to place a point on a circle for each one; let’s call this the hash ring.
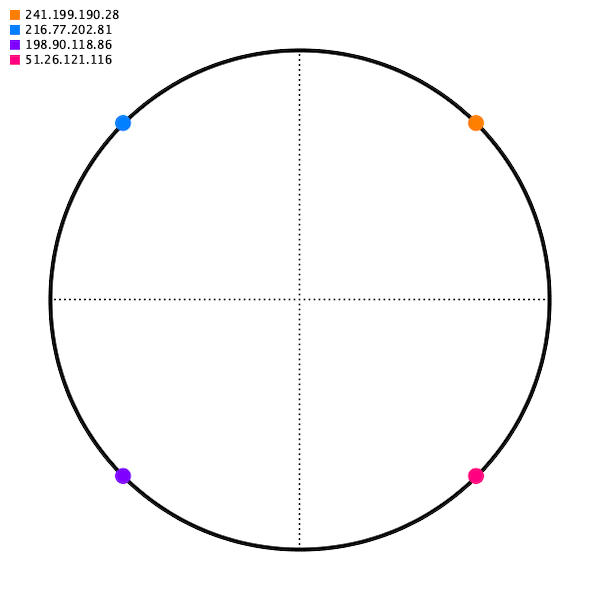
And then for some source IP address, we will map it to some point on the circle. For our mapping function, choose just the closest point going to the right (apparently this calculation can be done in O(logn) with a Red-black tree, but that’s more than I hope to accomplish today).
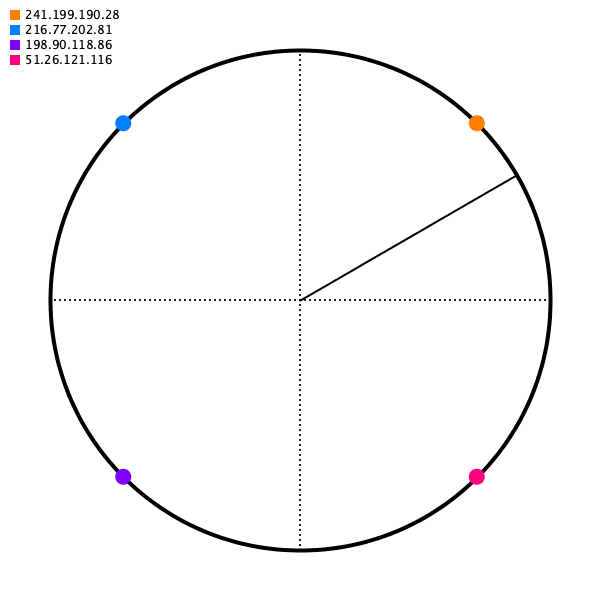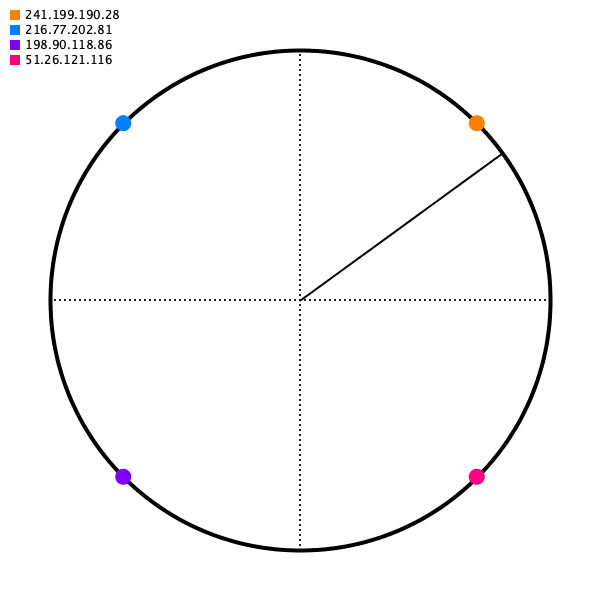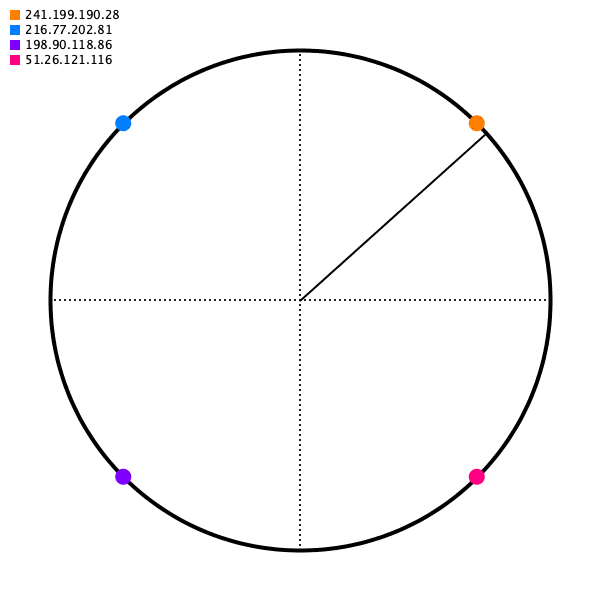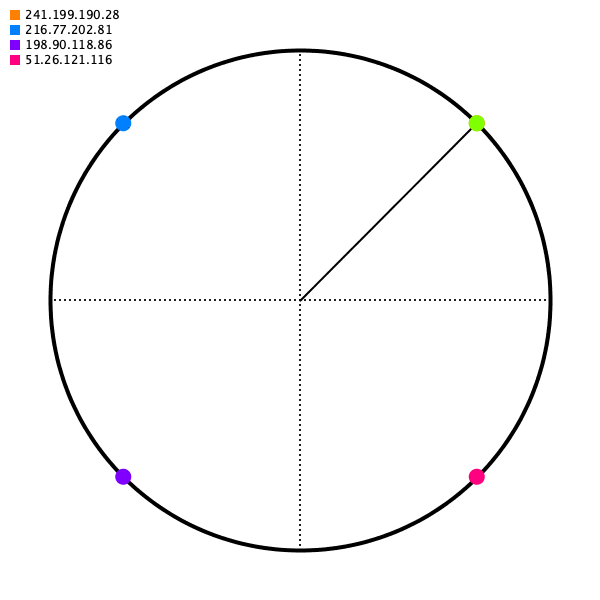
As long as the angle generated for some source IP is deterministic, we’ll get the same destination server.
Ok, so how do we place the server points on the circle? Common sense would say distributed evenly. But remember the constraint — when you add or remove a server, you can’t redistribute traffic. So if we started with 3 servers and added a 4th, we’d end up in this awkward situation, with the added server receiving just one sixth of traffic (which would be half of what the blue and purple server are receiving).
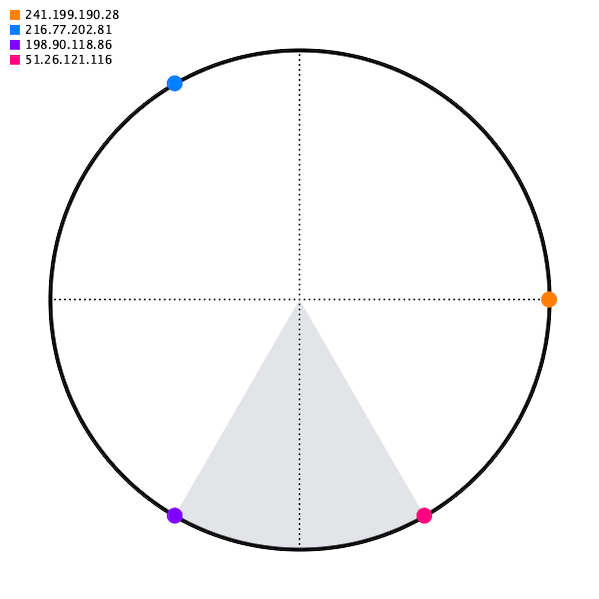
And removing a server is even worse.
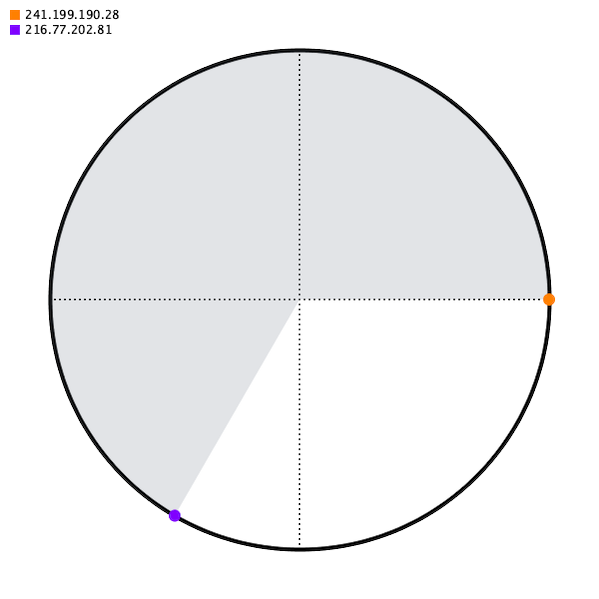
It turns out, the best way to distribute the points on the circle is randomly, with lots of redundancy.
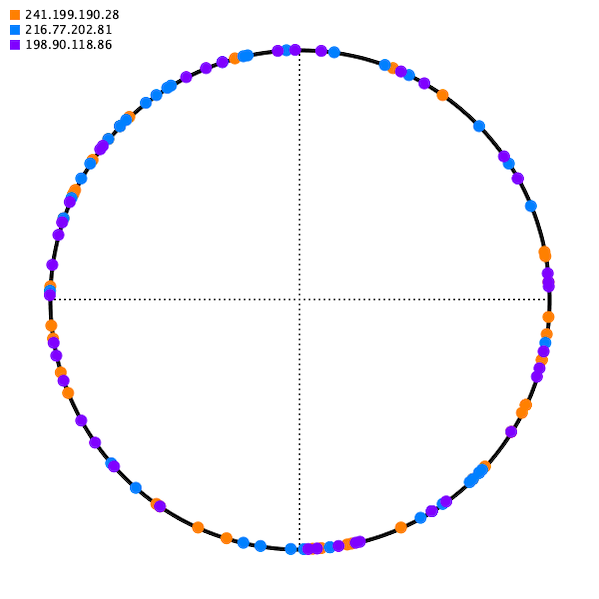
This way, when a server is added, you add n points randomly to the hash circle, and it receives an approximately equal amount of traffic, and only the traffic that is diverted to the new server is affected.
The same can be shown for when we remove a server. The added load on the remaining servers is distributed evenly.
Code
For the first problem, we need to consistently generate an angle. First we would convert the source IP to an integer. Then we just need a deterministic function that given some integer, returns an angle.
One way to do that is by taking advantage of the pseudo-ness of psuedo-random functions. Use the input as the seed, and get the first number in the sequence.
// GetAngle deterministically returns a value between 0 and 359func GetAngle(input int64) int { generator := rand.New(rand.NewSource(input))
return generator.Intn(360)}
func TestGetAngle(t *testing.T) { arr := []int64{2, 3, 5, 7, 11, 13}
for _, input := range arr { if GetAngle(input) != GetAngle(input) { t.Errorf("GetAngle(%d) is not deterministic.", input) } }}You could cache, but given the nature of distributed networking, holding a distributed cache for that probably wouldn’t be an option.
The other problem is, given an angle, return a server. I’m perfectly fine doing that through iteration (I’m using integers and so performance a pretty small number of iterations, especially when you consider how many points would be on a hash ring built with redundancy).
var hashRing = make(map[int]string)hashRing[45] = "241.199.190.28"hashRing[135] = "216.77.202.81"hashRing[225] = "198.90.118.86"hashRing[315] = "51.26.121.116"
// GetID returns an id given an anglefunc GetID(hashRing map[int]string, angle int) (string, error) { for i := 0; i < 360; i++ {
index := (angle + i) % 360
if hashRing[index] != "" { return hashRing[index], nil } }
return "", errors.New("the angle map passed in contained no values within 360 degrees of the angle")}If you actually do use this somewhere, do more research, and use a balanced binary search tree for the looking up of an IP given an angle.
Conclusion
19 years ago to the day, about 25 minutes before American Airlines Flight 11 crashed into the World Trade Center, the man in seat 9B was stabbed.
He had been a member of an elite Israeli counter-terrorism unit, and had at least a cursory understanding of Arabic—but we can only speculate as to why he was targeted.
That man was 31-year old Danny Lewin, one of the creators of consistent hashing.
Additional Reading
Wow! You read the whole thing. People who make it this far sometimes
want to receive emails when I post something new.
I also have an RSS feed.