A directed acyclic graph is one of the most important data structures we deal with in software engineering. You can’t understand Git without grasping the main concepts of this data structure. In the next four articles, we’re going to go in depth into this powerful data structure, and see why it sits at the heart of so many things.

A graph is a data structure, defined by its vertices and edges. Oftentimes you’ll see it defined as G = (V, E). That just means, “G is the graph defined by vertices V and edges E”.

We usually draw them like this:

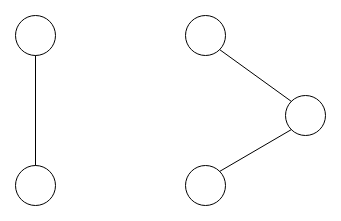
We call a graph connected if there is a path from any vertex to any other vertex.

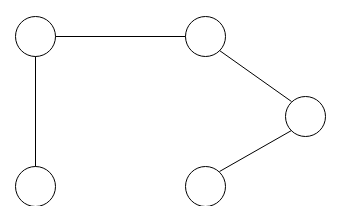
A cycle in a graph is a path from a vertex back to itself, where each edge is only travelled once (the above graph does not contain a cycle).

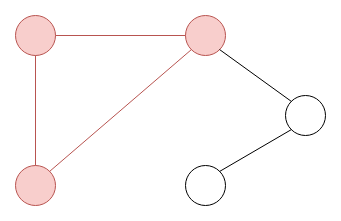
In a directed graph, each edge has a direction, meaning it goes from one vertex to another vertex. We draw directed graphs like this.

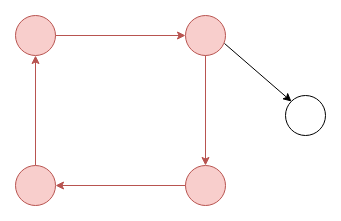
Directed graphs can have cycles too, like the above one in red. When a directed graph doesn’t have a cycle, we call it a directed acyclic graph (a DAG). (The changed edge to remove the cycle is shown in gold).

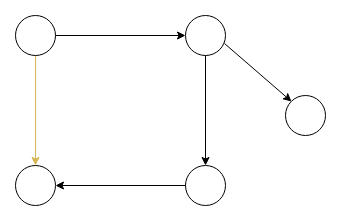
In short, that is a directed acyclic graph. A graph that is directed and has no cycles.

And what is a tree?

A related but different concept is a tree. A tree (in graph theory) is a graph where there is exactly one path from any vertex to any other. Or, more formally, a connected, undirected, acyclic graph.

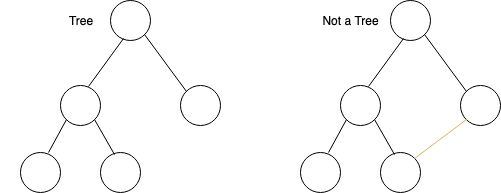
Think of a family tree.

We’ll dive deeper into the DAG in articles to come.